OpenGL is the standard API for cross-platform 3D graphics. With OpenGL you can create hardware-accelerated 3D graphics on a range of operating systems, including Windows, Linux, Mac OS X and Android. OpenGL takes advantage of a machine's Graphics Processing Unit (GPU) for fast rendering. In OpenGL, 3D shapes are made up of of individual triangles, each of which has three vertices (points making up the triangle).

Important OpenGL concepts

OpenGL coordinate system

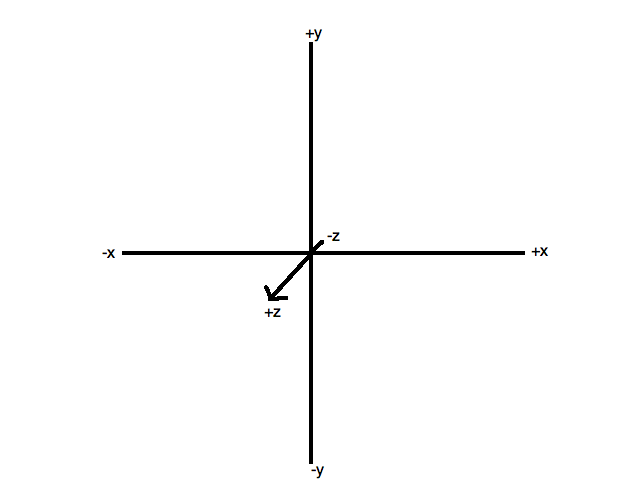
Since OpenGL is a 3D API, it uses three coordinates: x, y and z. It's important to realise that x increases to the right, and y increases upwards, This is different to the situation in 2D computer graphics, where y increases downwards - but is the same as in standard maths.

Because this is 3D graphics, we have a third axis, the z axis. You can think of this as pointing out at you from the screen, so that positive z coordinates are "in front of the screen" and negative z coordinates are "behind the screen". This is shown in the diagram below.

OpenGL and OpenGL ES

OpenGL ES is a version of OpenGL optimised for devices with limited resources, such as mobile devices (although these days many mobile devices have capabilities comparable with traditional desktop machines!) OpenGL ES programming is slightly different to standard OpenGL: it is somewhat more complex but more efficient. There are various versions of OpenGL ES: we will use OpenGL ES 2.0 as it provides what we need.

The API is significantly different to standard OpenGL. Drawing shapes takes on a different approach: rather than drawing each triangle individually, all vertices making up a complex shape are sent direct to the graphics card at once, in a buffer, for fast, efficient drawing.

The world and eye coordinate systems

When working with OpenGL, we have two coordinate systems. An OpenGL application typically comprises a virtual world which we can wander around, as a player in a game or a user of a VR or AR app. World coordinates define the position of objects within this virtual world. We also have the eye coordinate system. This describes the coordinates of objects with respect to the user's current view of the world, which may not be the same. We expand upon the difference below.

Typically, the coordinates of 3D objects in an OpenGL application will be specified in our code, or more commonly, in an external data source such as a file or the web. The coordinates of these objects are with respect to our virtual world, and can be thought of as the "true" coordinates of the objects within our 3D world - thus they are world coordinates. They define the absolute position of each object in our virtual world - in that respect they are conceptually similar to latitude and longitude. However, our view of the coordinates might be different. Imagine the origin of the 3D world is the central room in a 3D game. We might not be at that position in the world, we might be in a completely different room, and furthermore, we might not be looking down the negative z-axis as in the default view. We might be looking in a direction aligned at 45 degrees to both the x and z axes, as shown in the diagram below. Additionally, we might be on a slope, in which case, the up direction does not correspond to the y axis.

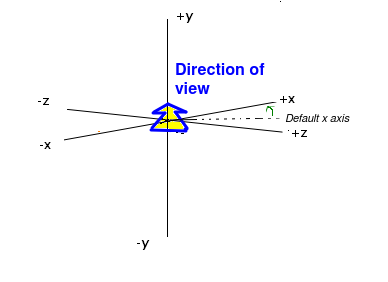
The current on-screen 3D coordinates of a given object, with respect to the user's current view, are the eye coordinates of that object. The eye coordinate (0,0,0) is always the user's position within the world. And in eye coordinates, we are always facing negative z, with x increasing to the right and y increasing upwards, even if we are not facing negative z in world coordinates.

When rendering 3D shapes, we use eye coordinates, because we want to render them with respect to the current view. Thus we have a problem, because the shapes will typically be stored in a file or on the web as world coordinates. So we have to define a transformation to convert the world coordinates to eye coordinates. This transformation has two components:

• A translation, to translate the coordinates from the world system to the eye system.
• A rotation, to rotate the field of view from the direction currently being faced in world coordinates into facing negative z in eye coordinates.

The camera

In many 3D applications, we want to allow the user to navigate through a 3D world, e.g. (as we have seen) a game or a VR or AR app. In these cases, we define the objects making up the world (which might include 3D buildings, terrain, points of interest, etc) in our code as world coordinates. We then define a camera, which represents the user's position in the world and the direction in which they are facing. Such a camera would have a set of world coordinates defining its position within the world, as well as a rotation. Such a camera, representing the user's position, is known as a first-person camera; other types of camera also exist which present a view of the world from the perspective of something other than the user (e.g. from the perspective of a certain room in a game, or a non-player character).

The world coordinates of the camera would vary, as the camera moves round the world. However, because a first-person camera represents the user's position, its eye coordinates will always be x=0, y=0, z=0.

Translating and rotating the camera

As seen above, the camera has a position and rotation. In more detail, it has:

• A defined position in the world (cx, cy, cz), as world coordinates;
• A defined set of rotations about each of the three axes in our world (x, y and z)

• Firstly, the camera is translated so that it is at position cx=0, cz=+2;
• Secondly, the camera is rotated by 90 degrees anticlockwise.

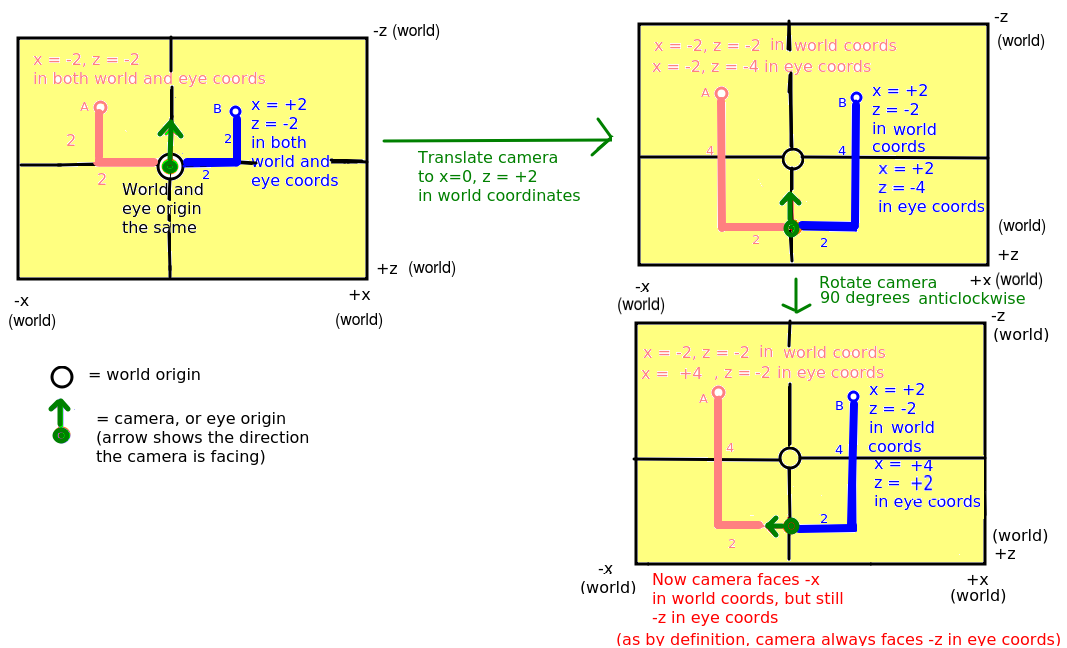
We are going to examine how the eye coordinates of points A and B change as we move the camera.

• Initially, the eye coordinates of A and B are equal to their world coordinates, as the camera is at the default position;
• When we move the camera to cx=0, cz=+2, the difference in z coordinates between the camera and the two points increases from 2 to 4.. In other words, with respect to the camera, or in eye coordinates A and B both have z coordinates of -4. The camera is at cz=+2, and still facing negative z, so points A and B both have z coordinates of -4 as they are both in front of the camera and four units away in the z direction. The world z coordinates of A and B, by contrast, are still -2: world coordinates do not change unless the objects move to a different position within the world (e.g. a monster moving in a game)
• We then rotate the camera by 90 degrees anticlockwise. This is done around the y-axis as shown in the diagram below:
  
  By doing this, the camera is now facing -x in world coordinates. However, in eye coordinates, the camera is still facing -z, as it always does this by definition.
• As a result, A and B are now both to the right of the camera, rather than in front of it. They are still both 4 units away from the camera, as the camera position has not changed (only its rotation), but since they are 4 units to the right of the camera (rather than in front), the eye x coordinate of both is +4 (rather than the eye z coordinate being -4 as was the case originally). Remember that by definition, in eye coordinates, positive x is always to the right.
• The eye z coordinates of A and B will now differ, as A is now in front of the camera and B is behind the camera. Consequently, A will have a negative eye z coordinate and B will have a positive eye z coordinate. As both A and B are two units distance along the eye z axis, it follows that the eye z coordinate of A will be -2 and the eye z coordinate of B will be +2.

Don't get confused by the word "camera"!

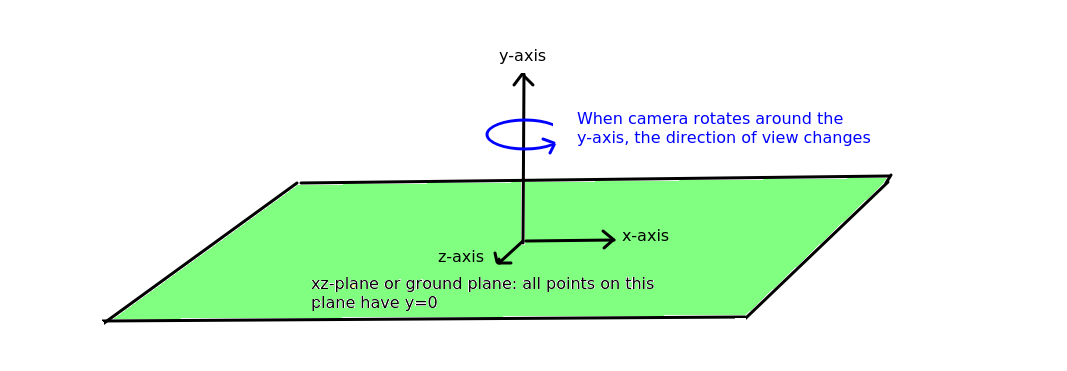
It's important to not get confused by the terminology here. The first-person OpenGL camera is not the same as the actual hardware camera used to take pictures on the device. When we move onto AR, we will use the term "hardware camera" to distinguish the physical camera from the OpenGL camera.

World and Eye Coordinates Demo

See here.

Matrices

Many of you will have come across matrices in the past, at school or college. Matrices are two-dimensional arrays of numbers which are most commonly used to represent geometric transformations which can be applied to shapes (both 2D and 3D), such as rotation, translation, magnification, stretch and shear. There are also other, more specialised, applications of matrices in science and maths - but these are out of the scope of this module. We will not go into the maths of matrices in great detail, but you need to be aware that a matrix represents a geometric transformation of some kind, such as translation or rotation. You also need to be aware of various matrices which exist within OpenGL which are involved in the rendering process. We will expand upon matrices a little next week.

The view matrix

OpenGL defines a matrix which specifies the transformation between the world coordinates and the eye coordinates. This is called the view matrix. Every time you do a translation or rotation in code, the view matrix is multiplied by the matrix which defines that rotation/translation. Then finally the coordinates specified in code (the world coordinates) are multiplied by the view matrix to give the coordinates with respect to the user's current view.

The projection matrix

The other type of matrix which is used in OpenGL is the projection matrix. This transforms the coordinates of shapes to add a sense of perspective, in other words it makes nearby shapes appear larger and further-away shapes appear smaller. So, shapes with eye z coordinates close to 0 (e.g. -1, -2) will appear relatively large, whereas shapes with negative z coordinates further from 0 (-10, -20, etc) will appear smaller. Without the projection matrix, no perspective is applied and shapes would appear the same size irrespective of their eye z coordinate. In fact, the exercises this week will not involve the projection matrix, and therefore, even though you will be doing some OpenGL programming the shapes you draw will appear flat, without a sense of perspective.

Architecture of a Android OpenGL ES 2.0 application

An Android OpenGL ES 2.0 application consists of:

• Standard Android code to process user events and communicate with servers if necessary
• Shaders running on the GPU to control rendering

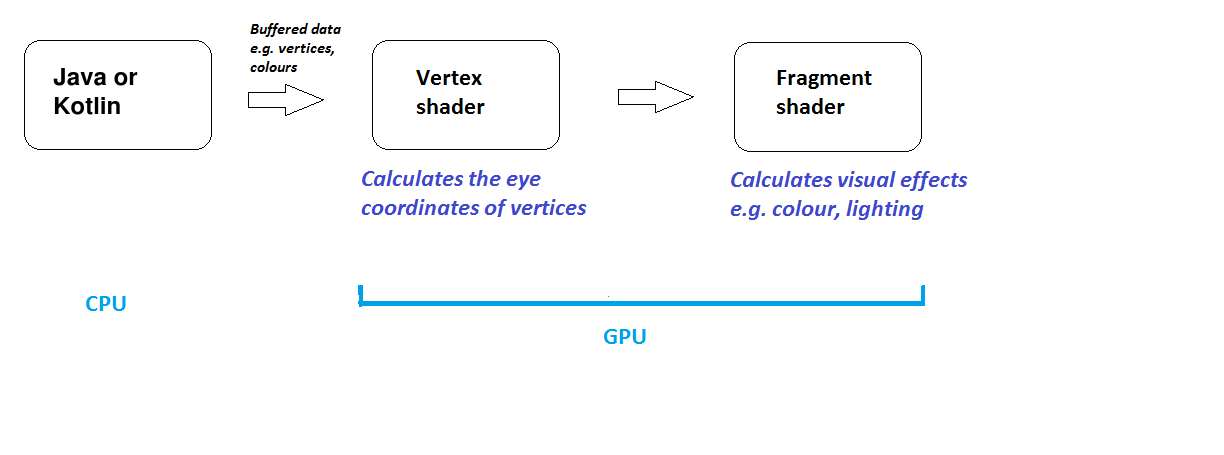
Android OpenGL ES 2.0 applications thus take place partly on the CPU and partly in the GPU (via shaders). A Android OpenGL ES 2.0 application generally works in this way:

• Kotlin or Java responds to user events by changing variables holding the position of objects in the 3D scene, or the user's current position in the world and the direction they are facing;
• These changes are then communicated to shaders on the GPU which actually do the rendering

Shaders

This discussion applies to OpenGL ES in general; not just Android OpenGL ES 2.0.

Android OpenGL ES 2.0 (and all OpenGL ES 2.0 implementations) require the use of shaders. Shaders are small programs, written in a C-like language, GLSL (GL Shader Language), which run on the graphics card (GPU) and specify how vertices, and thus shapes, appear on the screen (position, colour, lighting, textures etc). A shader-based OpenGL application will consist of a CPU based program plus a series of shaders running on the GPU. The CPU program passes information to the shaders through a process known as the rendering pipeline.

Types of shader

There are two types of shader:

• Vertex shaders: specify where vertices appear on the screen, in particular, how they are transformed from world space to eye space and how perspective is applied.
• Fragment (or pixel) shaders: determine how individual pixels appear on-screen (colour, lighting effects, etc)

Shader variables

There are three classes:

• Attribute variables: for quantities which vary for each vertex (e.g. vertex position)
• Uniform variables: for quantities which remain the same per render (e.g. the matrix representing the current rotation/translation of the scene, the drawing colour)
• Varying variables (to be covered later)

Example of a vertex shader

attribute vec4 aVertexPosition;
void main(void)
{
    gl_Position = aVertexPosition;
}

• This shader sets the position of the current vertex (gl_Position; this is a built-in GLSL variable) to the attribute variable aVertexPosition.
• The attribute variable aVertexPosition (data type vec4; this is an inbuilt GLSL data type) will contain the current position from the vertex buffer;each vertex from the buffer in turn is sent to the vertex shader.
• In our Kotlin code we link the buffer with the aVertexPosition variable, as we will see later.
• This example does not apply the view or perspective matrix: we will look at these below.

Example of a fragment shader

void main (void)
{
    gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);
}

• This is a simple fragment shader. All we do is set the colour of the current fragment (area of pixels on the screen surrounding a given vertex) to red (RGB 1,0,0; the fourth argument is the alpha - transparency - component)
• gl_FragColor is an inbuilt GLSL variable representing the current fragment colour. Note the use of vec4 again.

A fragment shader using a user-defined colour

In this example we read in the colour from the uniform variable uColour.

precision mediump float;
uniform vec4 uColour;

void main(void)
{
    gl_FragColor = uColour;
}