
This week we will look at two more specialised data structures, the linked list and the stack.
We will start with a look at linked lists. Linked lists, which are different to the plain lists we discussed last time, are unlike arrays or lists in that they are not stored continuously in memory. Instead, data is stored as a series of linked nodes. Each node contains one item of data, and links to the memory locations of the previous and the next item of data in the linked list.

Each node has a link to the previous and the following node. When we add a new item of data, we make the previous node link to the new node, and we link the new node back to the previous node to form a two-way link.
The first node in the list links to nothing in the reverse direction (indicated in Python by the special value None) and similarly, the final node in the list links to nothing in the forward direction.
What are the consequences of this?
Remember how we could use simple arithmetic, using the array index, to calculate the location in memory of a given element in an array or list. Can we do this here? We cannot. This is because, in a linked list, items are not stored continuously in memory. Instead, each node contains references to the memory locations of the previous and the following node.
On the other hand, as long as we have a reference to both the start and the end of the linked list, it's efficient to add a new member to the end of the linked list. We can just create a new node and link it, both ways, to the end node. Contrast this to arrays, in which we had to create a new array with additional space and copy the elements over. We will explore this in more detail in the exercises this week.
Insertion into the middle of the list has mixed efficiency. On the one hand we have to find the index we want to insert the element at (which as we saw above is inefficient), on the other hand the actual insertion process is easier as we can just break the existing links between the node BEFORE the element we want to insert and the node AFTER this element, and then link in the new element. Again we will look at this in the exercises.
A stack data structure involves adding items from bottom to top, rather like a stack of plates. When we remove items from the stack, we remove from the top, again just like a stack of plates. The stack is known as a "last in first out" or "LIFO" data structure. It is called this, because the last things we add to the stack, are the first things we remove. Here is an example of a simple stack of numbers.
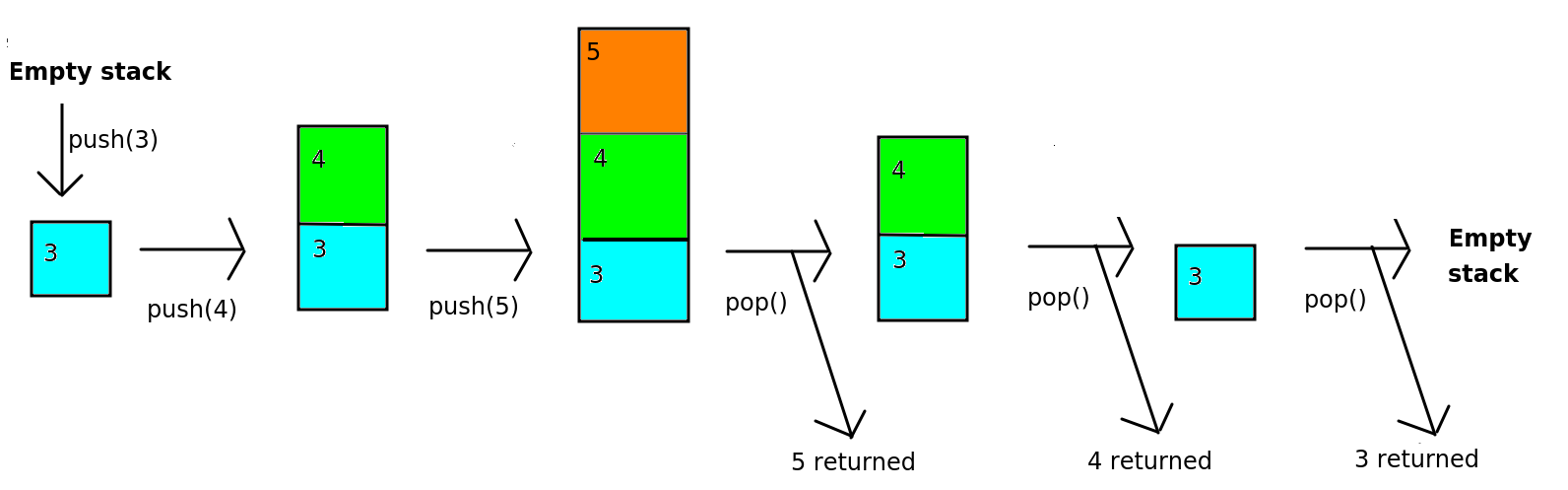
A stack can be used for any operation in which we need to navigate back to a previous state. Examples could include:
Browser navigation. When we visit a website, we often need to navigate back to a previous site. When we click the 'Back' button, we want to return to the site immediately preceding the one we are currently viewing. So when you click 'Back', the current site might be removed from the stack so that you return to the previous site.
Directory/folder structure. When navigating the folder system of your computer, you typically start at a 'root' folder (for example C:\ on Windows, or your home directory on Linux) and then navigate to subfolders, for example C:\Pictures. You then might navigate to a sub-sub-folder, such as C:\Pictures\Holiday and then C:\Pictures\Holiday\2018 and so on. In a subfolder you can navigate upwards to the previous folder, so that if you are in C:\Pictures\Holiday and you navigate upwards, you arrive at C:\Pictures and then C:\ if you navigate upwards once more. So the process of navigating upwards removes the current folder from the stack and returns to the previous folder.
"Undo" commands in desktop applications. Each action you take in a desktop application might be stored on a stack, so that if you select "Undo", the topmost operation would be reversed, and then removed from the stack.
(In actual fact, each of these is now implemented in a slightly more complex way, in the sense that you can, in modern browsers, move both back and forwards along your history, but we are assuming a more simplified implementation in which you can only move back for the purposes of illustrating a stack).
Another use of stacks, which you will appreciate more when you have done more programming, is:
The two key operations of a stack, adding and removing items, have special terms.
Push. To push an item onto a stack means to add it to the top. It is possible the stack may only have a certain capacity, i.e. it can only hold a certain number of items (perhaps due to memory constraints) in which case an error occurs if the stack is full.
Pop. To pop an item off the stack means to remove it from the top. The item is removed, and we also obtain it as a result of the pop operation. If the stack is empty, an error is generated.
An additional operation is:
Stacks are typically implemented using an internal array or list. When we push an item to a stack, we add an item to the next available space in this internal array. When we pop an item from a stack, we remove it from the last occupied space in the internal array, and "blank out" that position in the internal array.
When coding a data structure or algorithm, it is useful to be able to work out the logic of the code before you actually write any real code. Why is this useful?
Starting with a basic example, "Hello World" might look like this in pseudocode:
Print "hello world"Moving on to a more interesting example, here is some pseudocode to represent some simple logic to determine if you are old enough to vote:
Read age from the user into a variable "age"
If age is 18 or greater
Print "You are old enough to vote"
Otherwise
Print "Sadly you are not old enough to vote, but you will be in "
Print 18 minus age
Print "years"
And here is some pseudocode to represent a "while" loop to count up to a number that the user enters:
Read a number from the user into a variable "number"
Set a variable "counter" to 0
While counter is less than number
Print counter
Increase counter by 1
As can be seen, these examples of pseudocode represent the logic before we actually write code. They are trivial examples, but hopefully are enough to illustrate the point, and once completed, the pseudocode can then be implemented in real code of any given programming language. Python actually resembles pseudocode more than some other languages, so hopefully converting pseudocode to Python should be quite an easy job!
It should also be said that there are differing levels of detail that you can write pseudocode with. The examples above include references to variables, which make them particularly useful for converting into real code. For simple algorithms, you can go straight to this stage. In more complex algorithms you might want to, before you go into this level of detail, write some higher-level pseudocode which describes the general logic without referencing variables. This helps you think about the overall high level logic of what must be done before you start thinking about what variables are needed. Higher-level pseudocode for the age tester might look like this:
Read age from the user
If user's age is 18 or greater
Tell them that they are old enough to vote
Otherwise
Tell them that they are not old enough to vote
Tell them how long they must wait to vote, based on their age
Think about what you would have to do to search for a particular item in a linked list using its index, starting at the beginning.
Draw out a linked list containing the 5 items of data:
- Linux
- Windows
- Mac OS X
- Android
- iOS
Imagine we wish to retrieve the item with index 3 (Android). How could we do this? Draw out how you think it could be done on paper, and ask yourself: how efficient is this, particularly compared to doing the same thing with an array or list.
We are now going to perform another paper-based exercise with stacks, to help you understand them and their operations.
Imagine you have an empty stack. Draw the stack after each operation below, and explain what, if anything is returned from each operation and any errors that might occur.
push (a), push (b), pop (), push (c), peek (), pop (), pop (), pop (), push (d), push (e), push (f), pop (), push (g), push (h), peek (), push (i), pop (), pop (), pop (), peek ().
This exercise will allow you to think about the logic of stacks and linked lists using pseudocode, before you actually write real code. In two weeks' time, once you have learnt more Python programming, you will actually implement stacks and linked lists using real Python code.
First try writing, in a text editor, using pseudocode, the logic for implementing a stack.
push and pop operations on the internal array.
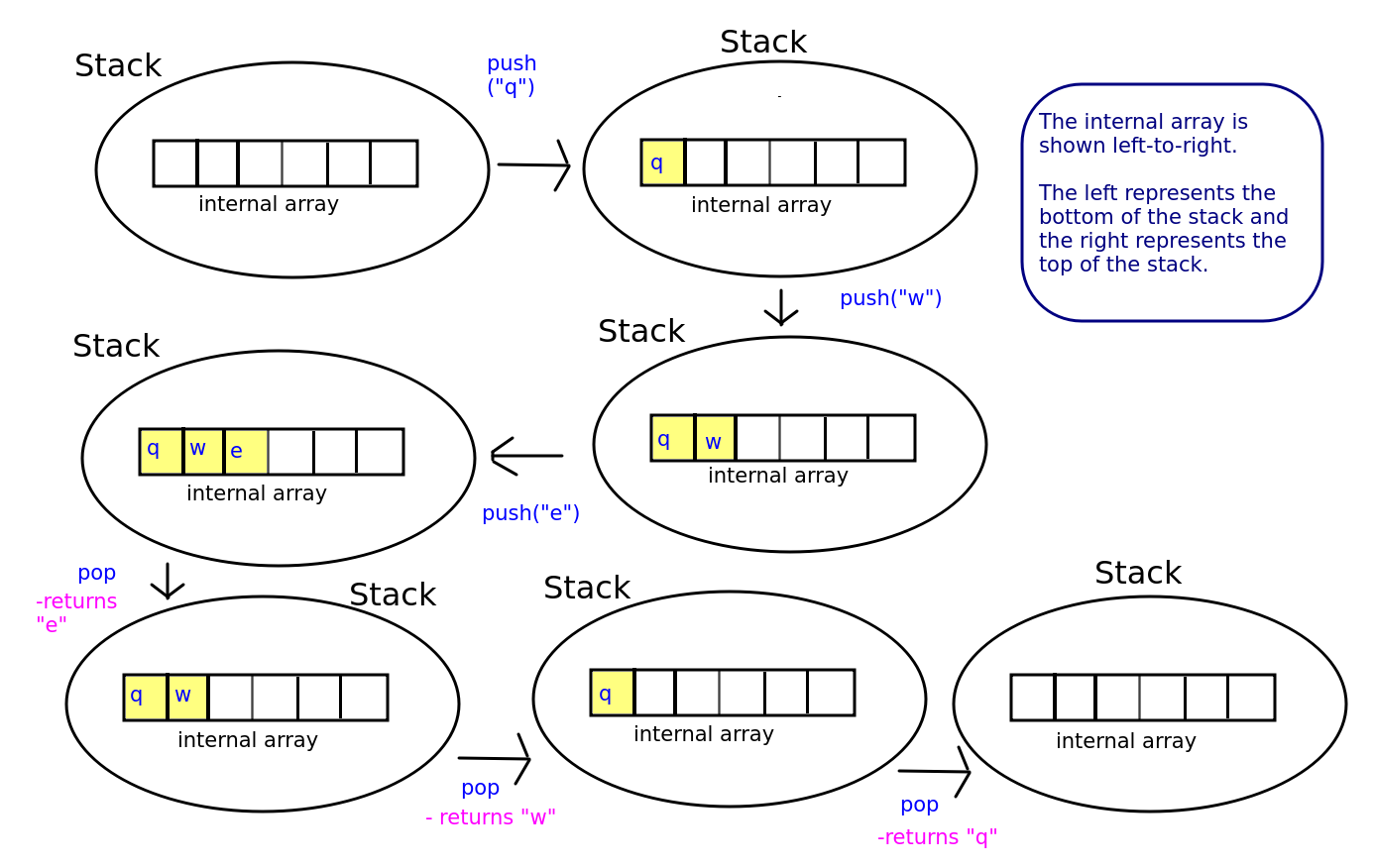
If you're struggling with the pseudocode, try writing higher-level pseudocode, without the use of variables, first. See the discussion on pseudocode above.
Try writing, in a text editor, using pseudocode, the logic for implementing the "add" and "get" operations of a linked list.
Advanced: write pseudocode for a third operation, "insertAt". This should insert a node into the linked list containing some data, after a given index. So if index 2 is specified, the node would be added after index 2.
If you're struggling with the pseudocode, try writing higher-level pseudocode, without the use of variables, first, as described above.